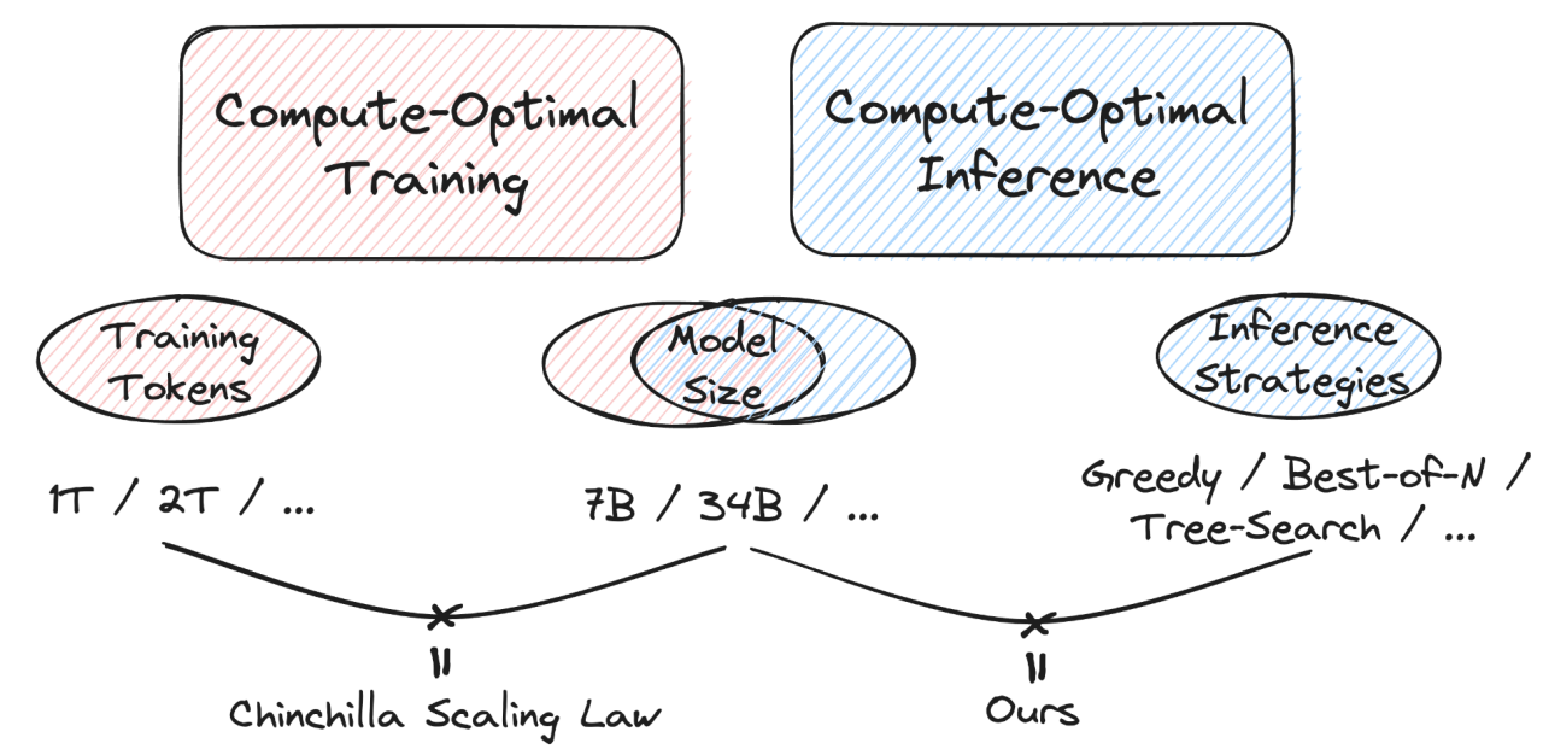
Inference Scaling Laws: An Empirical Analysis of Compute-Optimal Inference for Problem-Solving with Language Models

Abstract

While the scaling laws of large language models (LLMs) training have been extensively studied, optimal inference configurations of LLMs remain underexplored. We study inference scaling laws and compute-optimal inference, focusing on the trade-offs between model sizes and generating additional tokens with different inference strategies. As a first step towards understanding and designing compute-optimal inference methods, we studied cost-performance trade-offs for inference strategies such as greedy search, majority voting, best-of-$n$, weighted voting, and two different tree search algorithms, using different model sizes and compute budgets. Our findings indicate smaller models (e.g., Llemma-7B) can outperform larger models given the same computation budgets, and that smaller models paired with advanced inference algorithms yield Pareto-optimal cost-performance trade-offs. For instance, the Llemma-7B model, equipped with our novel tree search algorithm, consistently outperforms Llemma-34B with standard majority voting on the MATH benchmark across all FLOPs budgets. We hope these findings contribute to a broader understanding of inference scaling laws for LLMs.

Inference-compute Scaling

More model parameters may lead to high performance on various tasks, but what about scaling the number of decoding tokens in inference? By measuring the amount of computation in FLOPs and studying model performance across different sizes and inference strategies as computation scales up, we can gain a deeper understanding of the effect of inference scaling.

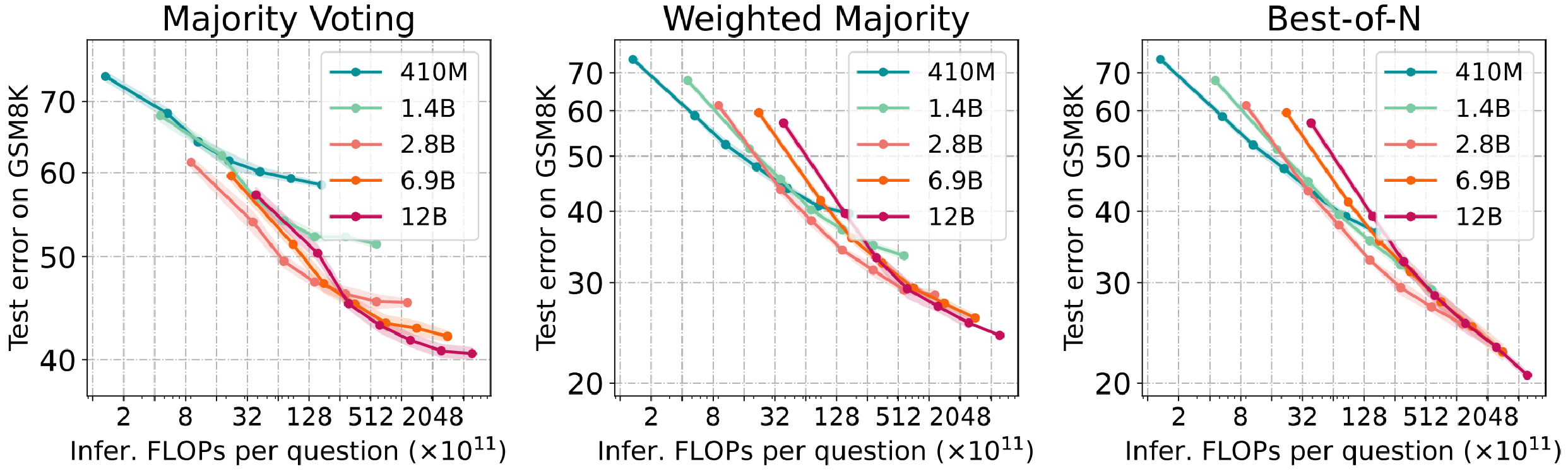
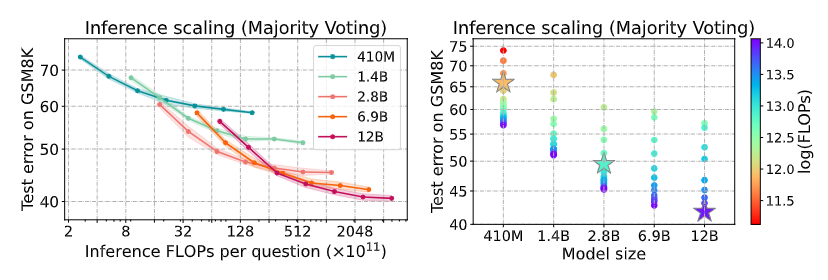
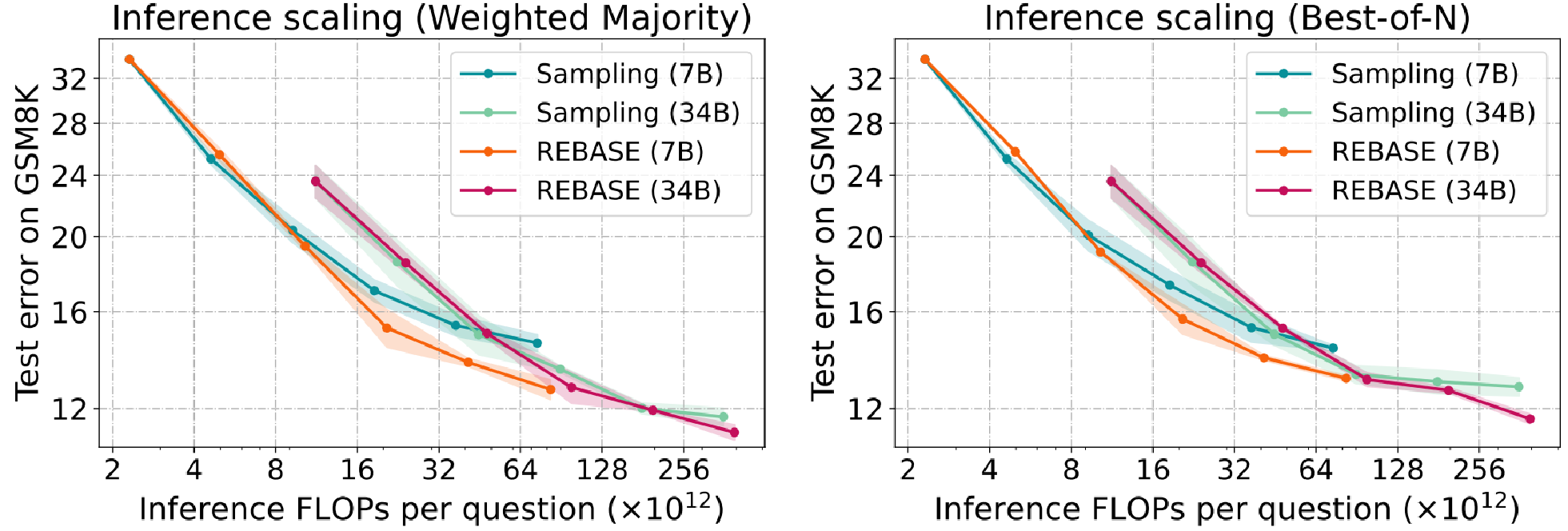
The error rate versus computation budget(in Flops), we evaluate the Pythia models on the GSM8k dataset accross different model sizes.

The *right* panel shows the model performances given inference FLOPs budgets. In particular, the three stars highlight the optimal model size under $10^{12}$, $10^{13}$, and $10^{14}$ FLOPs, indicating that the optimal model size can vary given different budgets.

Key findings:

Scaling inference compute by sampling more solutions leads to growing task performance.
Across all scenarios, there is an eventual point at which the accuracy will reach a plateau, indicating that additional computational resources yield diminishing returns.
The ideal model size varies depending on the available computational budget. Notably, smaller models tend to perform better when the compute budget is constrained.
We also provide theoretical analysis which shows the upperbound and convergence rate in our paper, find more infomation in our paper!

Compute-optimal Inference

In our paper, we also define the problem of compute-optimal inference, investigate the inference strategies that achieve high performance with a fixed compute budget.

We introduce REward BAlanced SEarch (REBASE) which is Pareto optimal compared to sampling. We have the following findings:

Sophisticated inference strategy like REBASE is compute-optimal.
Smaller models equipped with advanced inference strategy outperforms larger ones.

Citation

If you find our paper useful, please consider citing us.

@misc{wu2024inferencescalinglawsempirical,
  title={Inference Scaling Laws: An Empirical Analysis of Compute-Optimal Inference for Problem-Solving with Language Models}, 
  author={Yangzhen Wu and Zhiqing Sun and Shanda Li and Sean Welleck and Yiming Yang},
  year={2024},
  eprint={2408.00724},
  archivePrefix={arXiv},
  primaryClass={cs.AI},
  url={https://arxiv.org/abs/2408.00724}, 
}